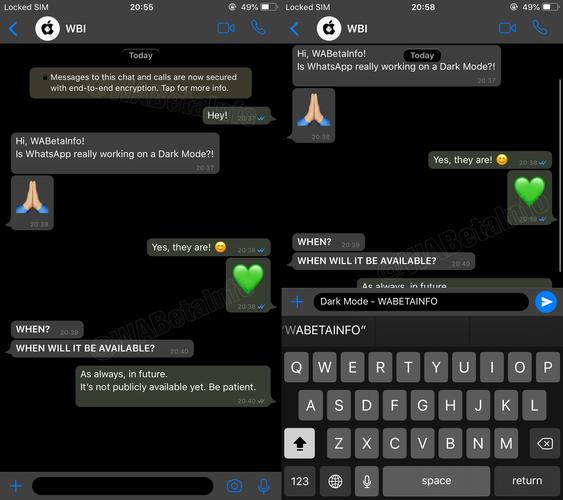
标准答案来了 x=-q2q2^2+p3^3^12^13+-q2+q2^2+p3^3^12^13详细的看这里 一元三次方程的求根公式用通常的演绎思维是作不出来的,用类似解一元二次方程的求根公式的配方法只能将型如ax^3+bx^2+cx+d+0的;一元三次方程的求根公式涉及多种方法,如配方法卡尔达诺方法韦达替换和拉格朗日方法,以及三角解法和几何解释这些方法通过变量替换对称多项式表达和三角函数技巧,将复杂的三次方程转化为更易处理的形式例如,配方法先通过立方变换消去次高次项,然后通过变量平移简化为没有二次项的方程卡尔达诺方法。
1 虚数的引入是为了解决负数平方根的问题在数学中,负数没有实数平方根,因此当判别式小于零的二次方程出现时,它没有实数解2 数学家卡尔达诺是首先引入虚数的人他将纯虚数表示为负数乘以虚数单位尽管他对此感到矛盾,一方面认为虚数是虚构的无实质内容,但另一方面也认识到虚数“比无实质;1736年,瑞士的欧拉出版力学或解析地叙述运动的理论,这是用分析方法发展牛顿的质点动力学的第一本著作1742年,英国的麦克劳林引进了函数的幂级数展开法1744年,瑞士的欧拉导出了变分法的欧拉方程,发现某些极小曲面1747年,法国的达朗贝尔等由弦振动的研究而开创偏微分方程论1748年,瑞士的。
随着时代的演进,三角学逐渐发展成为一门独立的数学学科14世纪时,中亚数学家阿勒·哈姆什被公认为三角学的先驱他建立了弦表,并成功应用弦表解决了实际问题随后,16世纪德国数学家卡尔达诺和纳拉多等人进一步推动了三角学的发展,他们的研究成果为三角学的广泛应用奠定了坚实基础进入17世纪,三角函。
卡尔达诺cardano项目
1、在初中阶段,我们对实数有了深入理解后,数学的奇妙之旅引领我们进入了“虚数”的神秘领域这一概念源于意大利数学家卡尔达诺的大术,他首次揭示了虚数的存在,将它与实数共同构成我们今天熟知的“复数”复数域的构建,不仅由笛卡尔赋予了清晰的定义,拉斐尔·邦贝利更进一步完善了虚数乘法,构建出一个。
2、代数基本定理是数学中基础且重要的一环,它断言任何复系数多项式方程在复数域中至少有一个根这一定理有多种等价表述,其中一个表示是任意复系数多项式在复数域上必定存在一个一次因式代数基本定理的演变始于17世纪,当时讨论方程根的数量问题吉罗拉莫·卡尔达诺是首个意识到三次方程可能有三个根。
3、数学在文艺复兴时期迎来了重要的发展阶段这一时期的数学家们在方程求解方面取得了显著成果,特别是三次和四次方程的解法意大利数学家卡尔达诺在其著作大术中发表了三次方程的求根公式,但其实这一公式的发现应归功于塔尔塔利亚卡尔达诺的学生费拉里发现了四次方程的解法,并在大术中有所记载。
4、如果说他和别的孩子有什么不同的话,那就是他的动手能力相当强他做过会活动的水车做过能测出准确时间的水钟还做过一种水车风车联动装置,它使风车可以在无风时借助水力驱动15岁那年,一场罕见的暴风雨侵袭英格兰狂风怒吼,牛顿家的房子直晃悠,就像要倒了似的牛顿为大自然的威力迷住了。
5、定理意义韦达定理在求根的对称函数,讨论二次方程根的符号解对称方程组以及解一些有关二次曲线的问题都凸显出独特的作用一元二次方程的根的判别式为 a,b,c分别为一元二次方程的二次项系数,一次项系数和常数项,韦达定理与根的判别式的关系更是密不可分根的判别式是判定方程是否有。
6、除了喜帕恰斯,古印度数学家也对三角函数有所贡献大约在公元5世纪,印度数学家阿耶波多编制了早期的三角函数表,这标志着三角学在印度的发展古希腊的球面三角学和古印度的三角函数研究,为后来的数学家奠定了基础随着时间的推移,这些早期的工作逐渐演变成现代的三角函数理论直到16世纪,卡尔达诺和韦达。
7、古希腊的数学家,比如毕达哥拉斯和他的学派,对有理数的发展做出了重要贡献他们提出了“毕达哥拉斯定理”,即直角三角形斜边平方等于两直角边平方之和这个定理为有理数的研究提供了重要的理论依据到了16世纪,意大利数学家卡尔达诺提出了“卡尔达诺公式”,这个公式首次将有理数和无理数联系起来。
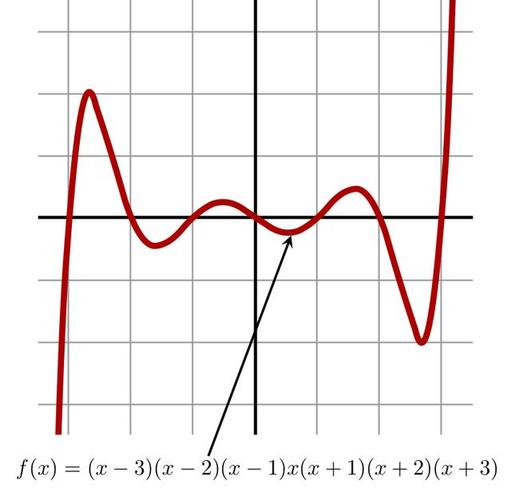
什么叫卡尔达诺函数图像
1、虚数已经成为微芯片设计和数字压缩运算的核心工具你的M P3播放器就依赖虚数比这更重要的是,虚数是带来电子学革命的量子力学的基础没有复数,现代技术几乎不可能存在而复数包含实数,也包括虚数16世纪,意大利数学家杰罗洛莫·卡尔达诺发现虚数时,就连负数都在遭受强烈的怀疑尽管这都是难弄的。
2、高等代数不是高等数学 ,两者区别如下一指代不同 1高等代数代数在讨论任意多个未知数的一次方程组,也叫线性方程组的同时还研究次数更高的一元方程组2高等数学 是由微积分学,较深入的代数学几何学以及它们之间的交叉内容所形成的一门基础学科二特性不同 1高等代数高等代数是。
3、Ouroboros使用公开验证秘密共享方案实现领导者选举Ouroboros Praos利用可验证随机函数作为核心随机生成方案,进一步提升领导者选择过程的公平性和透明性实际应用与发展卡尔达诺主网Ouroboros算法已在卡尔达诺主网上实际使用,并计划逐步过渡到更先进的Ouroboros Praos算法未来规划随着卡尔达诺网络的发展。